터널 수치해석 모델 (유한요소, 유한차분) + 내공변위제어법
ENGINEER/토목-Civil터널의 해석순서
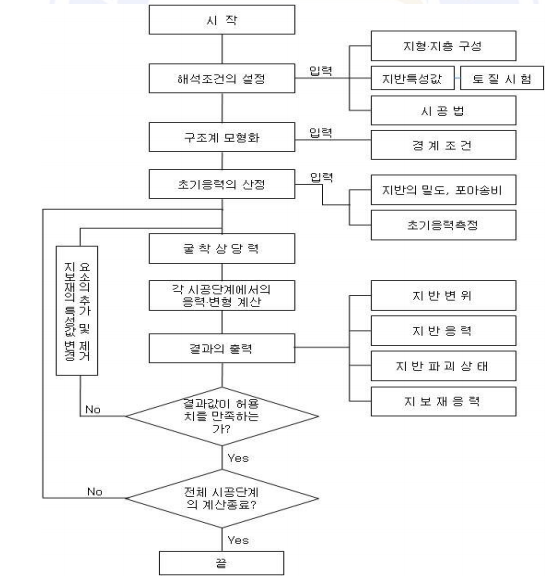
단순 한계평형, 내공변위 해석 및 계측에 의한 역해석에서
수치해석을 적용하게 되면서,
- 탄소성모델, 점탄성모델, 점탄소성모델 등 적용 가능
- 지반의 이방성, 불균질성, 비선형성, 불연속성 등 재료의 특성도 반영하여 해석 가능
- 시공 단계별 Simulation 가능 – 거동 예측

Kirsh 의 해 : 원형에만 적용 가능
- 응력의 재배열. 탄성영역/소성영역 구분 및 소성평형
- 초기 (r=a) 와 K0 값의 변화에 따라 탄성변형. (측벽과 천단부) 측벽 변형량이 더 크다.
- r/a 가 커질수록 (소성영역에서 탄성영역으로 갈수록) K0 는 전단과 수직응력이 1:1로 수렴(K0에 관계없이)
해석모델의 종류
1. 유한요소법
- 요소와 절점으로 구성하여
- 응력-변형률 관계를 이용한 해의 정의
- 복잡한 지반조건의 해석, 불균질성 해석, 시간의존성 해석 가능
- 시간이 오래 걸리고, 저장량이 필요하며, 모델을 작성하는 사람의 숙련도나 지식이 필요.
- 경계조건 설정이 중요함.
2. 유한차분법
- 유한요소법과 비슷하나, 미지수의 해법이 시간 단위의 기준으로 동적해석이나 시간당 변화량 등에 적용됨.
- 계산 시간이 짧고 저장용량이 적으며 미소변형 뿐 아니라 대변형의 해석이 필요.
3. 경계요소법
- 마찬가지로 지반을 연속체로 간주하고
- 경계부분만 해석하고, 선형 거동에 유효한 해석방법
- 시간의 변수 등을 적용하기 어려움.
4. 개별요소법
- 지반을 각각의 강성블록으로 생각하고 진행.
- 핵석을 떠올리고
- 절리의 변위가 블록 자체의 변위보다 큰 경우 적용 가능.
5. 혼합법

수치해석은 경험적 방법(RMR, Terzaghi, Q-system 등) 과 비교될 수 있다.
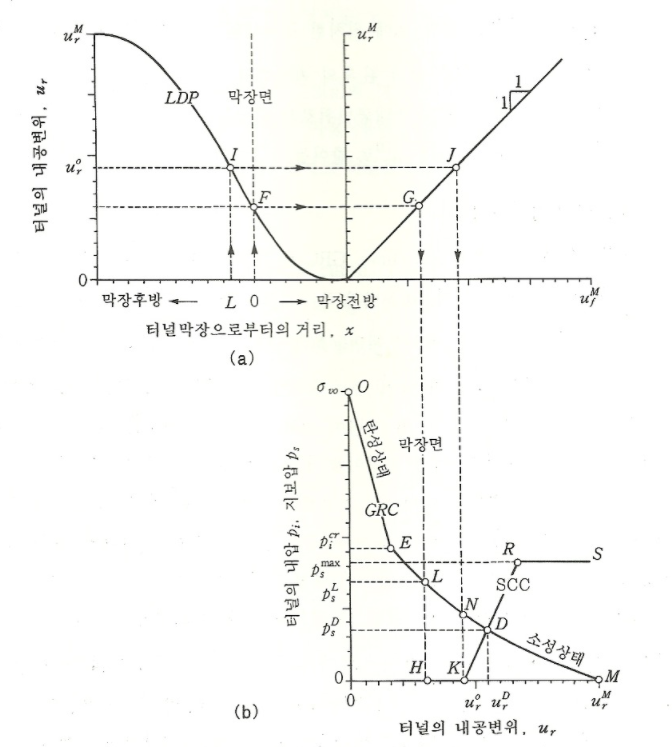
내공변위 제어 방법 원리 3가지. (LDP 종단변형, GRC 암반반응, SCC 지보특성)
'ENGINEER > 토목-Civil' 카테고리의 다른 글
| 침출수 투수성 반응벽체 (PRB) (0) | 2021.05.21 |
|---|---|
| 해상 풍력발전 기초 (0) | 2021.05.20 |
| 암반의 일반 수정하중, 절리면, 암반분류 (Terzaghi, Rose) (0) | 2021.05.20 |
| 깎기부 발파 시 유의사항 (소음, 진동, 비석) 진동추정식, 탁월주기 (0) | 2021.05.19 |
| 점토의 연대효과 (Aging Effect) (0) | 2021.05.18 |