전단 특성의 차이는 배수와 확산이중층 존재에 따른 점착력이라고 볼 수 있다.

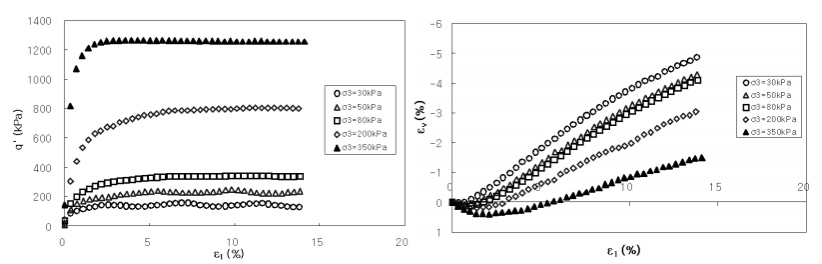
사질토의 전단

-       마찰각에 따른 마찰력이 중요. (입자간의 Interlocking, 엇물림 현상)
-       수직응력의 재하에 따라 차이가 커짐
-       활동마찰(느슨), 회전마찰(조밀)
-       전단-변형률 곡선의 차이. 항상 느슨과 조밀의 차이를 보여주는 것이 중요. (점성토는 NC/OC)
-       영향요소 : 간극비, 상대밀도, 최대건조단위중량, 입자의 형상과 입도분포, 구속압력(커지면 오히려 꺾이면서 전단저항각이 작아짐)

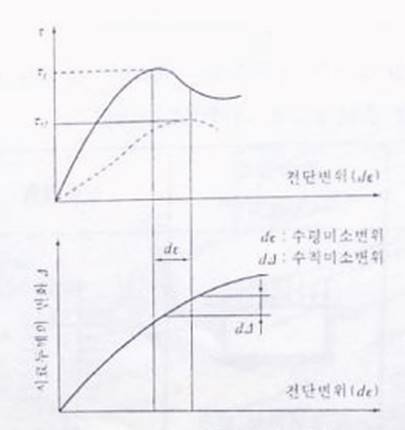
점성토의 전단

-       삼축압축 시험의 종류별 Mohr-Coulomb 시험으로 설명할 수 있음.
-       확산이중층, 동형치환, 배수, 점착력
-       파괴를 일으키는 과잉간극수압에 주목할 필요가 있음.
-       포화도에 따른 차이도 주목
-       정규압밀, 과압밀 (점착력의 발현)

OCR 이 커지면 응력경로 상, 초기에는 체적 팽창 경향이 있다가 체적 감소 경향을 보인다.

조밀 사질토의 경우 Dilatancy 현상에서처럼 시험 중 하중 재하 단계에서 축변형률이 커질 수록 체적 팽창의 형상을 보이는 것처럼
OC (OCR>2) 상태에서는 이런 모습을 보인다고 할 수 있다.
구속압이 작을수록 체적 팽창은 커진다.

기본적인 Dilatancy 의 모습.


전단시험에서의 Dilatancy 보정 (다일러턴시)
흙의 팽창에 따라 발생된 두께차이 x 수직응력 = 전단응력 x 수평변위
이에 따른 전단응력을 계산하고 그를 제외하고 전단응력을 계산하면 다일러턴시를 제외한 시험결과가 얻어지며,
그에 맞는 c, pi 를 구할 수 있다.

침투력 흡인력 참조 : https://huedor2.tistory.com/m/771


불포화토와 포화토의 차이
- 간극수의 영향을 고려하지 않으나 실제로 고려가 필요하고 모세관 현상 등의 작용으로 포화토와는 다른 거동특성
- 부분포화(Partially saturated), 불포화(unsaturated) 라고 부름.
- 모관흡수력의 존재 여부가 가장 큰 차이.

사면
- 하부 배수가 발생하는 경우 윗부분의 불포화 현상. 모관흡수력(흡인력 존재), 겉보기 마찰력

불포화토의 함수특성곡선
- 함수특성곡선 : w(%)-흡인력(kPa) 곡선

1) 포화함수비에서 흡인력이 증가해도 물이 간극에서 유출되지 않는다.
2) Air Entry Value (AEV, 공기함입치, 보통 20kPa?) 를 초과하면서 공기 유입에 따라 물이 유출되고 흡수력이 같이 증가하게 됨.
3) AEV, 잔류함수량을 구하는 것이 목적.
4) 잔류함수비는 열에 의해서만 제거 가능.

불포화토의 전단특성
식 하나로 설명이 가능하고,

모관흡수력 ua – uw 는 내부마찰각이 아닌 겉보기마찰각을 사용한다.
겉보기 마찰각은 함수비/잔류함수비의 관계에 따라 내부마찰각과의 관계를 가질 수 있으며,
내부마찰각의 tan 값의 반정도가 된다고 볼 수 있음.

불포화토의 전단강도는 실험을 통해 얻기가 어렵다. (시간/장비/불포화상태의 구현)

이를 통해 강우 전/후의 사면의 안정을 수치해석으로 계산할 수 있으며,
그에 따른 대책 및 피해 정도를 예측할 수 있다.

Bishop 응력
- 수직응력과 모관흡수력의 선형적 조합.
- Bishop 의 유효응력
p = (p-ua) + K (ua-uw)
변수K 를 포화도로 볼 수 있고, 1인 경우 일반 전단특성과 동일.
- 축차응력 q 와 Bishop 응력의 비례관계.