직선 : 무한 사면. 지하수여부
원형 : 절편 (Fellenius), Bishop 법, 마찰원법 (Moment 평형)
절편사이 : Spencer, Janbu
대수나선 : Log Spiral.

1. Fellenius : 공극수압이 큰 완만한 사면 – 오류 발생. 과소설계. pi =0
2. Bishop : 원호활동에 적합. 간편법.(검증용으로 사용) Fellenius 와 동시 사용.
3. Janbu, Spencer : 평형조건을 만족시키는 방법

절편법

저면, 선단, 대수나선 등의 파괴를 유한 토사사면의 절편으로 나누어
안전율의 합을 계산함.

(1) Input : c,pi, unit weight, H, slope(angle), surcharge
(2) 이론

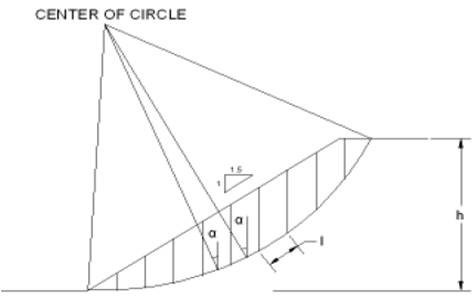
a(알파) 는 절편마다 달라진다.

(3) 공식

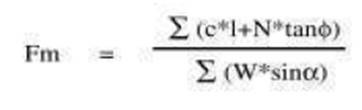
N = W cons a

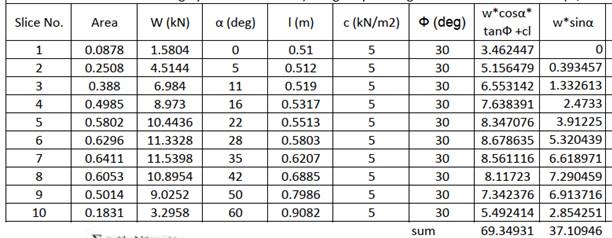
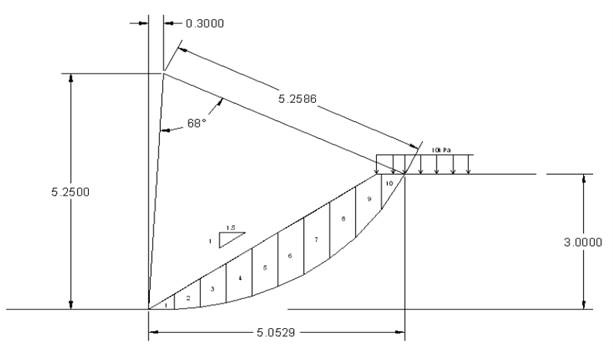
(4) Water Table 을 고려하는 경우

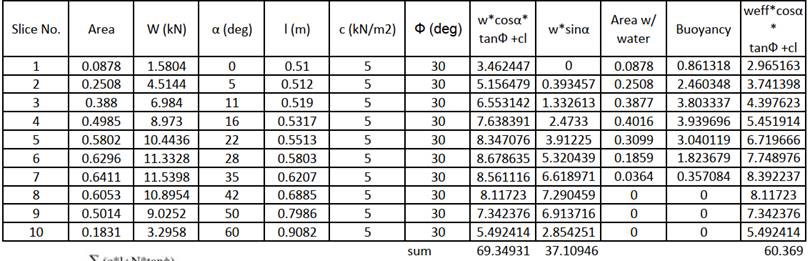
rsub 를 고려한 하중을 적용.

지반 해석 방법의 종류 (사면과 흙막이)

지반이 소성변형을 일으키면 조건들을 충족시키는 해석이 어려움. (극한해석법, 경계이론)

일부 조건만 충족시키는 근사법 접근이 필요.
- 가정사항 : 흙은 완전탄소성, 가상일의원리.
- 힘의 균형방정식, 변위의 적합조건식, 재료의 구성식, 경계조건식 충족 필요. (상한계, 하한계 이론)
- 상한계 : 힘에 관한 경계조건 무시. 파괴하중에 대한 상계치 구함.
- 하한계 : 변위의 경계조건 무시. 실제 파괴하중의 하계치. (파괴가 발생하지 않는 하중값)
- 파괴하중은 이 경계값 사이에 존재.
- 개념상의 차이와 적용에 따른 차이로 접근 필요.

한계평형법이 널리사용됨.
(파괴가 발생할 때의 힘의 균형으로부터 한계력을 계산, 위험한 파괴면을 찾는 방식, 근사해의 위치가 맞는지 확인이 어려움.)
단점 : 정해와의 관계가 불확실함.
장점 : 현장 상황과의 일치도가 높음.

이론은 장단점 위주로 접근이 필요.
그래야 오래 남는다.