압밀의 개념 (압밀방정식, 등시곡선, 시험, 계수, 1차원, 다차원)
ENGINEER/토목-Civil
압밀 단계
- 초기압밀 : 하중에 따름. (탄성 이론)
- 1차압밀 : 간극수압 소산, 유효응력 증가
(EOP, End of Primary)
- 2차압밀 : 소성 재조정
1차원 압밀모형
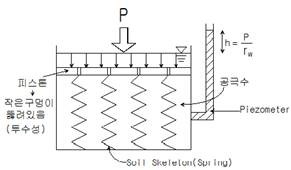
1차원 압밀 방정식 : 압밀/1차원/침하량/일이비균포간다/Terzaghi
- 1방향/횡방향구속, 2차원 무시
- 비압축, 균질, 포화, 간극수압/유효응력 반비례, Darcy (투수계수 일정)
- 유입량-유출량=체적변화율, Q=vz dx dy, aV/at, h=u/rw (하중을 가한 후 과잉간극수압 발생, 그에 따른 수위상승)
- mv = av /1+e, Cv = K/(mv rw)
- au/at = Cv a2u/az2 (속도에 대한 편미분, 유입 유출에 따른 V 를 체적변화계수와 섞은 편미분의 결합.)
- Tv=Cv t /H2 (미분방정식의 해를 통해 Tv 를 구하고 그에 따라 압밀도 연결.)
- 압밀도 그래프 (U=u0-u / u0), Z/Hdr(배수거리)=1.0 에서 최소 (중간이라고 생각, 양면배수 가정)
- 평균압밀도 U bar = 침하량/전체침하량. 그래프. Tv = pi()/4 U^2 (<60), 1.781-0.933 log(100-U) (면적에 의한 평균 압밀도 그림 기억 필요.)
- 2차 압축지수 S=Ca H log (t/t), 소성재배열, 압밀 시험에서 e-logt 경사 = Ca
- Sf=Si(Se)+Sc+Ss(Scr)

압밀 시험 : e-logP 곡선. 압축지수, 선행압밀하중, 체적압축계수(변형률), 압축계수(간극), 압밀계수
압밀 계수
sqrt t : d-sqrt(t) 곡선 작성 – 곡선연장 d0 – 1/1.15 배 기울기 (d90) – 총침하는 x 10/9
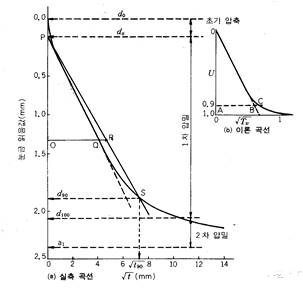
log t : 중간-마지막의 직선을 이은 교점 d100 – d0 계산 - 4t 계산하여 (t1 = 1분 가정) 중간값으로 계산 – d50 계산
응력이력에 따른 현장 처녀 압밀곡선
교점을 0.42e0 라고 가정한다. (C)
현장에서 구한 pc 와 e0 가 만나는 지점을 연결하여 현장처녀압밀곡선 작성.
(현장의 기울기가 크다. 침하량이 크다. 교란이 되면 침하량이 under-estimated 된다.)
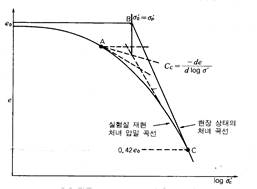
Pc 와 0.42e 기준 접선의 교점 : 현장 상태의 선행압밀하중
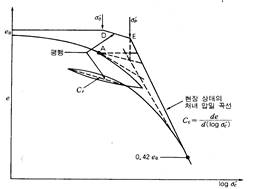
D 입력 Cr 기준으로 그린 선과 0.42e 의 접선의 교점 : 현장 상태의 선행압밀하중
2차 압밀 : 유기질, 예민, 해성점토는 40~50 % 까지 된다. (보통은 10~15%)
현장 적용 시 유의사항
- 조립토, 불포화토의 경우 실내시험에서 압밀이 적게 나오더라도 수침이 되는 경우 2차압밀이 많이 발생할 수 있으므로, 수침에 대한 압축성을 미리 예상할 수 있게 시험해둘 필요가 있다.
- 자중압밀에 대한 시간이 크게 나오는 경우, 침투압을 포함시켜 (수두차를 형성하여) 침투압밀을 유도할 수 있다.
- CRS : 하중 제어식이 아닌 일정변형률을 측정하는 변위 제어식 방법. 과연 선형으로 해석할 수 있는지 의문.
- 급속 압밀시험
- 배압(back pressure)을 통해 시료를 완전히 포화
- 1차원 압밀 방정식에서 간극수압이 아닌 변형률에 대한 미분 방정식 사용.
- 변형률 속도 산정이 중요
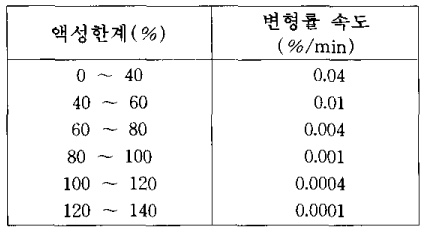
CRS (Constant Rate of Strain)
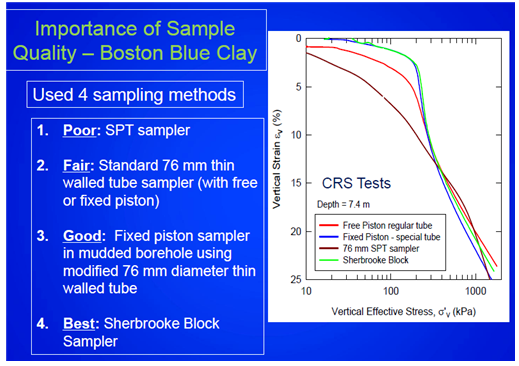
좋은 그림. 교란과 CRS 압밀을 동시에 설명할 수 있는
단계하중법과 등변형율법을 그림으로 비교하면 이렇게 될 수도 있겠네요.
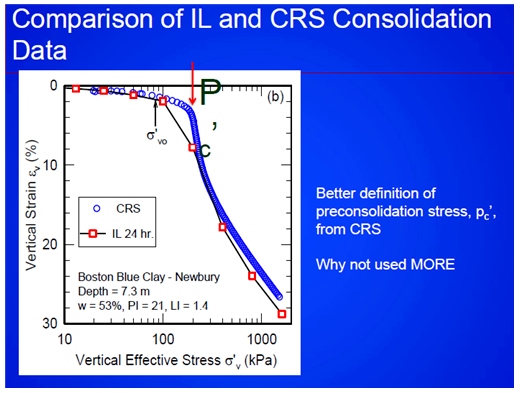

등시곡선 (Isochrone)
압밀 과정을 시간에 따라 나타나는 압밀도의 분포로 나타냄. (단면, 양면 배수)

다차원 압밀
- 축방향의 변형고려, 그에 따른 압밀량의 증감이 1차원과 다른 거동을 유도함.
- Terzaghi-Rendulic의 3차원 압밀이론
z 뿐만 아닌 x,y 가 포함되게 압밀 방정식을 유도하였고 Cv 가 투수계수의 차이에 따라 체적변화가 달라질 수 있음을 설명.
원통좌표계를 도입하여 압밀 방정식을 해석.
U = 1 – (1-uz)(1-ur) 을 통한 3차원 접근.
'ENGINEER > 토목-Civil' 카테고리의 다른 글
| 흙막이 토압 (경험 토압) (10) | 2021.04.06 |
|---|---|
| 계측의 주기 (굴착, 터널), 토사유출량, 탁도, 누수 (5) | 2021.04.05 |
| 대한민국 토질의 특성 (0) | 2021.04.02 |
| 침투력 Seepage Force 흡입력, 흡인력 (Matric Suction), 모관상승고 입경, 흙수분시험 (0) | 2021.04.01 |
| 부주면 마찰력, 강관파일 Goodman, 장경비, 중립점 (7) | 2021.03.30 |